Мастерство анализа функций: алгоритмы выявления промежутков возрастания и убывания

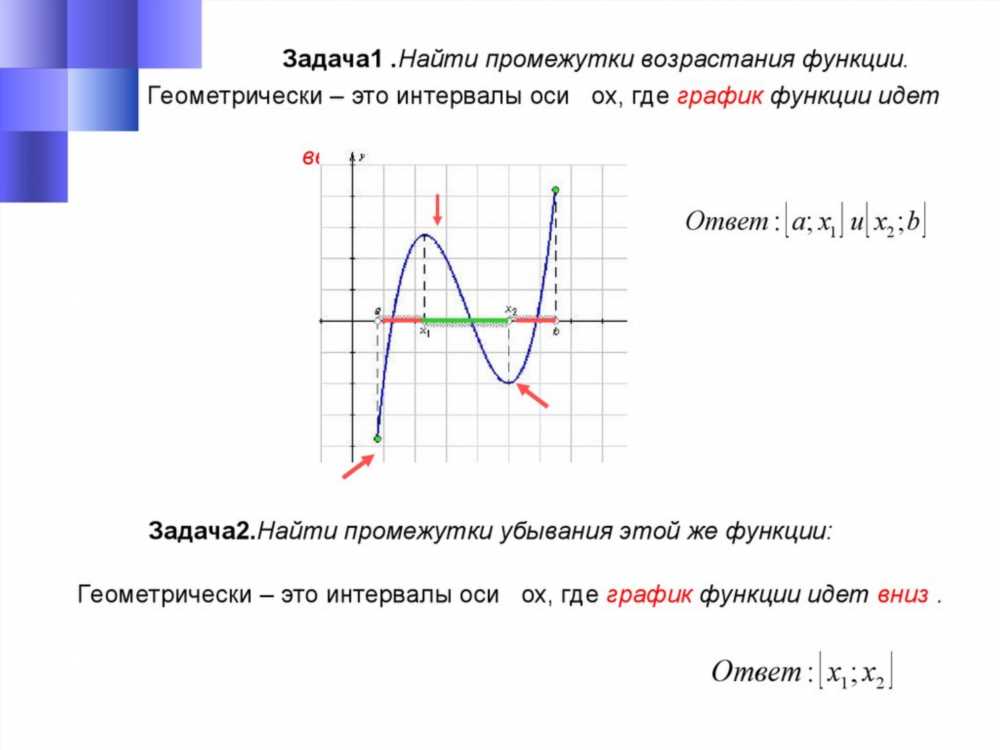
При изучении функций одной из важнейших задач является анализ их поведения на определенных интервалах. Особенно важным является определение промежутков, на которых функция возрастает или убывает. Это не только помогает понять глобальные тенденции функции, но и может быть критически важным при решении задач оптимизации, определении экстремумов и многих других приложениях. В данной статье мы рассмотрим алгоритмы, которые позволяют эффективно находить промежутки возрастания и убывания функций.

1. Понимание понятий: промежутки возрастания и убывания

Перед тем как перейти к алгоритмам, важно четко определить, что такое промежутки возрастания и убывания функции. Промежуток возрастания функции - это интервал, на котором значение функции увеличивается по мере увеличения аргумента. Аналогично, промежуток убывания - это интервал, на котором значение функции уменьшается по мере увеличения аргумента.

2. Использование производных

Один из наиболее распространенных методов для нахождения промежутков возрастания и убывания функций - использование производных. Для этого необходимо выполнить следующие шаги:

2.1. Нахождение производной функции

Первым шагом является нахождение производной функции, которая описывает ее скорость изменения в каждой точке. Для непрерывных функций это можно сделать аналитически или с помощью численных методов.

2.2. Определение знака производной

После того как производная функции найдена, необходимо определить ее знак на различных интервалах. Если производная положительна на некотором интервале, то функция возрастает на этом интервале. Если производная отрицательна, то функция убывает.

2.3. Выявление точек перегиба

Также важно выявить точки, в которых производная меняет знак. Эти точки могут указывать на экстремумы функции или на точки перегиба, где изменяется направление ее изменения.

3. Использование табличных данных

Для некоторых функций может быть удобно использовать табличные данные вместо аналитических выражений. В этом случае алгоритм поиска промежутков возрастания и убывания может выглядеть следующим образом:

3.1. Построение таблицы значений функции

Сначала необходимо построить таблицу значений функции на интервале, который необходимо проанализировать. Для этого можно выбрать равномерное разбиение интервала и вычислить значение функции в каждой точке.

3.2. Определение изменения значений

Затем следует определить изменение значений функции между соседними точками таблицы. Если значение функции увеличивается, то это может указывать на промежуток возрастания, а если уменьшается - на промежуток убывания.

3.3. Анализ результатов

После того как все значения проанализированы, необходимо проанализировать полученные результаты и выделить промежутки возрастания и убывания функции.

4. Сравнение методов и выбор подходящего

Каждый из описанных методов имеет свои преимущества и недостатки и может быть более или менее эффективным в зависимости от конкретной функции и задачи. Поэтому важно учитывать особенности функции и требования к точности при выборе метода.

Заключение

Анализ промежутков возрастания и убывания функций играет важную роль в математическом моделировании и решении различных задач. Понимание алгоритмов, позволяющих эффективно находить эти промежутки, помогает более глубоко понять поведение функций и использовать их в практических приложениях.