Все о площади поверхности прямоугольного параллелепипеда: формула, примеры и приложения

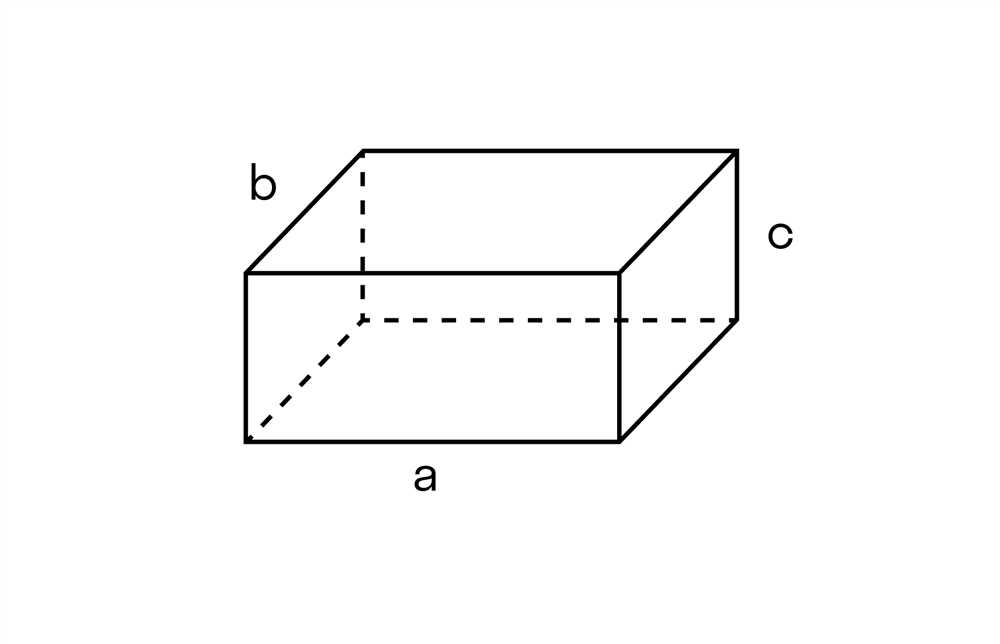
Прямоугольный параллелепипед – одна из базовых геометрических фигур, широко применяемая в различных областях, от строительства до математики. Его поверхность играет ключевую роль в расчетах и проектировании. В этой статье мы рассмотрим все аспекты площади поверхности прямоугольного параллелепипеда: от формулы до практических примеров.

Формула площади поверхности прямоугольного параллелепипеда

Площадь одной стороны: Для нахождения площади одной стороны прямоугольного параллелепипеда используется простая формула: $S_{side} = a imes b$ где $a$ и $b$ - длины двух сторон прямоугольника.

Шесть сторон: Прямоугольный параллелепипед имеет шесть сторон. Для нахождения общей площади поверхности необходимо найти площадь каждой стороны и сложить их: $S_{total} = 2ab + 2bc + 2ac$

Примеры расчетов

Пример 1: Допустим, у нас есть прямоугольный параллелепипед с длиной $a = 4$ см, шириной $b = 3$ см и высотой $c = 5$ см.

1. Найдем площадь одной стороны: $S_{side} = 4 imes 3 = 12 ext{ см}^2$
2. Теперь вычислим общую площадь поверхности: $S_{total} = 2 imes 4 imes 3 + 2 imes 3 imes 5 + 2 imes 4 imes 5$ $S_{total} = 24 + 30 + 40 = 94 ext{ см}^2$ Таким образом, площадь поверхности этого параллелепипеда равна 94 квадратным сантиметрам.

Пример 2: Рассмотрим еще один пример с размерами $a = 6$ см, $b = 2$ см и $c = 3$ см.

1. Площадь одной стороны: $S_{side} = 6 imes 2 = 12 ext{ см}^2$
2. Общая площадь поверхности: $S_{total} = 2 imes 6 imes 2 + 2 imes 2 imes 3 + 2 imes 6 imes 3$ $S_{total} = 24 + 12 + 36 = 72 ext{ см}^2$ Получаем, что площадь поверхности данного параллелепипеда равна 72 квадратным сантиметрам.

Приложения в реальной жизни

Строительство: Площадь поверхности прямоугольного параллелепипеда используется в строительстве для расчета необходимого количества материала, такого как кирпичи, плиты или обои.

Упаковка и транспортировка: Когда речь идет об упаковке и транспортировке различных товаров, знание площади поверхности параллелепипеда помогает определить оптимальный размер упаковки или грузового контейнера.

Математические модели: В науке и инженерии площадь поверхности параллелепипеда используется для создания математических моделей различных процессов и явлений.

В заключении, площадь поверхности прямоугольного параллелепипеда - это важный концепт, который находит применение в различных сферах. Знание его формулы и способов расчета может быть полезным как в учебе, так и в реальной жизни.